შექმენით თქვენი საკუთარი ლაბირინთი: კლასის აქტივობა რიცხვთა წრფეზე სეგმენტების ბუდეების გამოყენებით.

Original web-page: http://www.math.stonybrook.edu/~tony/mazes/demo1.html

ლაბირინთებიდან 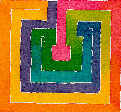მათემატიკამდე

ტონი ფილიპსი, მათემატიკის განყოფილება ნიუ-იორკის სახელმწიფო უნივერსიტეტი სტონი ბრუკი
tony at math.stonybrook.edu

ამ გვერდებზე აღწერილი აქტივობა შესაფერისია მე-6 კლასის მოსწავლეებისთვის. ახალგაზრდა სტუდენტებისთვის, სცადეთ ლაბირინთების შესწავლა.

ლაბირინთები (სიტყვა გამოიყენება აქ განსაკუთრებული სახის ლაბირინთისთვის) აშენდა და სარგებლობდა ხალხის მიერ პრეისტორიული დროიდან. ახლახან იპოვეს გზა ამ შაბლონების რიცხვით კოდირებისთვის და მათემატიკური ფორმულირების გამოსაყენებლად არსებული ლაბირინთების შესასწავლად და ახლის შესაქმნელად.

მონახაზი:

• პირველ რიგში სტუდენტები ისწავლიან კრეტის ლაბირინთის დახატვას. ეს 8 დონის ლაბირინთი ყველაზე ძველია; მისი გრაგნილების ნიმუში და უბრალო „ბირთვიდან“ წარმოქმნილი გზა კვლავ მომხიბვლელია.
• შემდეგ ისინი აღმოაჩენენ დონის თანმიმდევრობა ამ ლაბირინთის (ეს არის 0 3 2 1 4 7 6 5 8) და ნაჩვენები იქნება კრიტერიუმები, რომლებიც საშუალებას აძლევს რიცხვთა თანმიმდევრობას იყოს ლაბირინთის დონის მიმდევრობა.
• შემდეგ კლასი და მასწავლებელი ერთად გამოიყენებენ ამ კრიტერიუმებს 10 ან 12 დონის ლაბირინთის ასაგებად. ვინაიდან არსებობს 262 სხვადასხვა 10 დონის ლაბირინთი და 1828 სხვადასხვა 12 დონის ლაბირინთი, არსებობს შანსი, რომ მათი იყოს ისეთი, რომელიც აქამდე არასდროს უნახავთ.
• ბოლოს კლასი დახატავს თავის ახალ ლაბირინთს იატაკზე და პირდაპირ განიცდის მასში გავლისას.

მარაგი:

• თითოეულ მოსწავლეს უნდა ჰქონდეს ფანქარი და რამდენიმე ფურცელი. სასარგებლოა გრაფიკული ქაღალდის ფურცელი.
• დაფა ან OHP მასწავლებლისთვის. სასარგებლოა ფერადი ცარცი.
• გაზეთების ქაღალდი ან ყასაბანი 18 x 21 ფუტის ფართობის დასაფარად.
• 1.5 ან 2″ სიგანის ნიღბების ლენტი, სამი ან ოთხი სქელი მარკერი-კალამი.
• მუსიკა ლაბირინთისთვის: რაღაც ძალიან მშვიდი, როგორიცაა სატის “გიმნოპედიები”, ფორტეპიანოზე ან ჩაწერილი.

მდე შემდეგი გვერდი

დაბრუნება მთავარი ლაბირინთის გვერდი

დაბრუნება ტონის მთავარი გვერდი