Original web-page: http://www.math.stonybrook.edu/~tony/mazes/classify.html
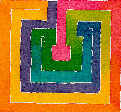
ლაბირინთებიდან მათემატიკაში
კლასიკურ და შუასაუკუნეების ლაბირინთების ტიპებს შორის არის განსხვავებული მარტივი ალტერნატიული სატრანზიტო ლაბირინთების მაგალითები იმავე რაოდენობის დონით. Მაგალითად
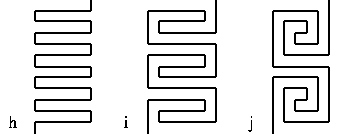
ეს სამი 12 დონის ლაბირინთის ბილიკები ხდება. ეს ბადებს კითხვას: რამდენი განსხვავებული ლაბირინთია იქ n დონეზე?
ახლა შესაძლებელია ჩამოვთვალოთ მოცემული სიღრმის n ყველა შესაძლო ლაბირინთები, 0,…, n ყველა პერუმაციის დათვალიერებით და მათი გაუქმებით, რომლებიც არ აკმაყოფილებენ სამ პირობას, რომლებიც გარანტიას იძლევიან, რომ თანმიმდევრობა შეესაბამება ლაბირინთს. ფაქტობრივად, ვინაიდან კოეფიციენტები და ლუწები არ შეიძლება შერეულ იქნას პერმუტაციაში და რადგან 0 და n უნდა დარჩეს ფიქსირებული, საკმარისია შევხედოთ ყველა წყვილი პერმატაციას, ერთ კენტი მთელ რიცხვს 1,…,n-1 (თუ ვიღებთ n ლუწს), და ერთ-ერთი რიცხვითი რიცხვი 2,…,n-2. მაგალითად, ყველა შესაძლო 8 დონის ლაბირინთების ასაშენებლად, თქვენ უნდა გაითვალისწინოთ წყვილი პერმაცია 1,3,5,7 და 2,4,6. არის 24 x 6 = 144 ასეთი წყვილი, ასე რომ ეს ადვილად შეიძლება გაკეთდეს ხელით. აქ არის ის, რაც შეიძლება აღმოვაჩინოთ 1-დან 8-მდე სიღრმეებში. ამ ჩამონათვალში გამოტოვებულია არა “საინტერესო” ლაბირინთები (ისინი შეიძლება აშენდეს უფრო ღრმა ლაბირინთებიდან ზედა და/ან ქვედა დონის ტრივიალური დონის დამატებით). ეს ფიგურა გვიჩვენებს ამ ლაბირინთების ბირთვებს და მართკუთხა ლაბირინთებს; თითოეული ორმაგი წყვილის მხოლოდ ერთი წარმომადგენელია დახატული.
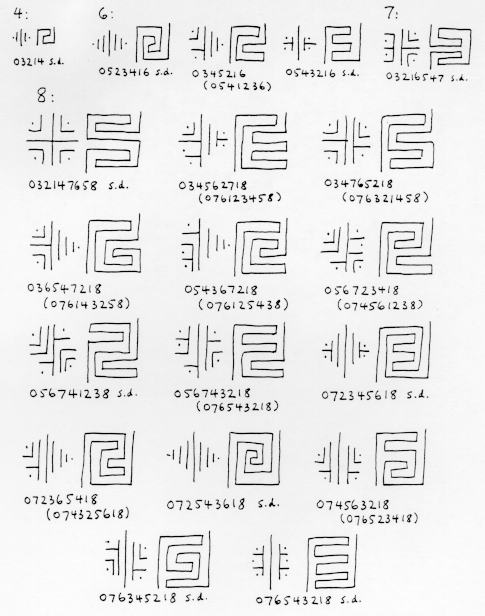
4,6,7 და 8 დონის საინტერესო ლაბირინთებიდან. თითოეული ორმაგი წყვილის მხოლოდ ერთი წარმომადგენელია დახატული. ს.დ.: თვითმმართველობის ორმაგი.
აქ მოცემულია მონაცემები ცხრილის სახით:
სიღრმე ლაბირინთების რაოდენობა საინტერესო ლაბირინთებიდან
1 1 არცერთი
2 1 არცერთი
3 1 არცერთი
4 2 03214
5 3 არცერთი
6 8 0523416 0543216
0345216 0541236
7 14 03216547
8 42 032147658 034567218 034765218
036547218 054367218 056723418
056741238 056743218 072345618
072365418 072543618 074325618
074561238 074563218 076123458
076125438 076143258 076321458
076345218 076523418 076541238
076543218
სიღრმის 9 -ისთვის უნდა განვიხილოთ 24 x 24 = 576 პერმუტაცია და შეცდომის შესაძლებლობები გაიზარდოს. შემდეგი რიცხვები გამოითვლება კომპიუტერების გამოყენებით.
n M(n) I(n)
1 1 0
2 1 0
3 1 0
4 2 1
5 3 0
6 8 4
7 14 1
8 42 22
9 81 11
10 262 142
11 538 95
12 1828 1014
13 3926 808
14 13820 7796
15 30694 6980
16 110954 63386
17 252939 61725
18 933458 538534
19 2172830 558853
20 8152860 4740658
21 19304190 5171300
22 73424650 42969130
24 678390116
26 6405031050
28 61606881612
30 602188541928
32 5969806669034
აქ M(n) და I(n) არის ლაბირინთების რიცხვი და n სიღრმის საინტერესო ლაბირინთებიდან. 24, 26 და 28-ის მნიშვნელობები მიიღო ჯიმ რიდსმა ბელის ლაბორატორიები–ის მიერ იმ მეთოდით, რომელიც არ ჩანს უცნაური სიღრმის რიცხვებზე. 30 და 32 მნიშვნელობები მოხსენიებულია ლანდოსა და ზვონკინის 1993 წლის ნაშრომში ვ. რ. პრატი–ის გამო.
საინტერესო 9 დონის ლაბირინთებიდან ეს ფიგურა ნაჩვენებია მათი მართკუთხა ლაბირინთის ბილიკებით; ისევ და ისევ, თითოეული ორმაგი წყვილის მხოლოდ ერთი წარმომადგენელია დახატული.
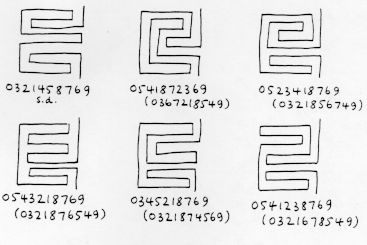
სიღრმის 11 საინტერესო ლაბირინთიდან 9.
მომდევნო ფიგურაში ნაჩვენებია ლაბირინთის ბილიკები 5 თვითმმართველობის ორმაგი ძალიან საინტერესო ლაბირინთებიდან 10 სიღრმეზე; ეს არის ლაბირინთები, რომლებსაც ასევე არ აქვთ ტრივიალური დონის შიდა მიმდევრობა.

5 ძალიან საინტერესო თვითმმართველობის ორმაგი ლაბირინთებიდან 10. სიღრმე 10. ნიმუშები, სახელწოდებით alpha_10 და გამა_10 გვხვდება რომაული მოზაიკის ლაბირინთებში.
დამატებულია 11/18/2009 0321654987.10 ასევე უნდა იყოს ამ ჯგუფში. მადლობელი ვარ ვალტერ დ პულენის ამ ინფორმაციისთვის.
დამატებულია 02/09/2018 0349852167.10 ასევე უნდა დაემატოს. მადლობა ანდრეას ფრეის!
როგორ გამოითვლება ეს რიცხვები?
რატომ დავინტერესდი ამ პრობლემით?
სხვაგან სად არის ეს რიცხვები?
კიდევ რა არის ცნობილი ლაბირინთის რიცხვების შესახებ?
ტონი ფილიპსი /Tony Phillips/
მათემატიკის დეპარტამენტი, მზიანი სტონი ბრუკი
tony at math.stonybrook.edu
1997 წლის 17 მარტი